肖特基二极管(SBD)
理想金属-半导体接触的 Schottky–Mott 理论
SBD 器件中包含两个电极:阳极和阴极,阳极是金属半导体的肖特基接触,阴极是金属半导体的欧姆接触,这两个金属电极的研制是 SBD 器件制备过程中的关键所在,下面介绍金属半导体接触的理论基础。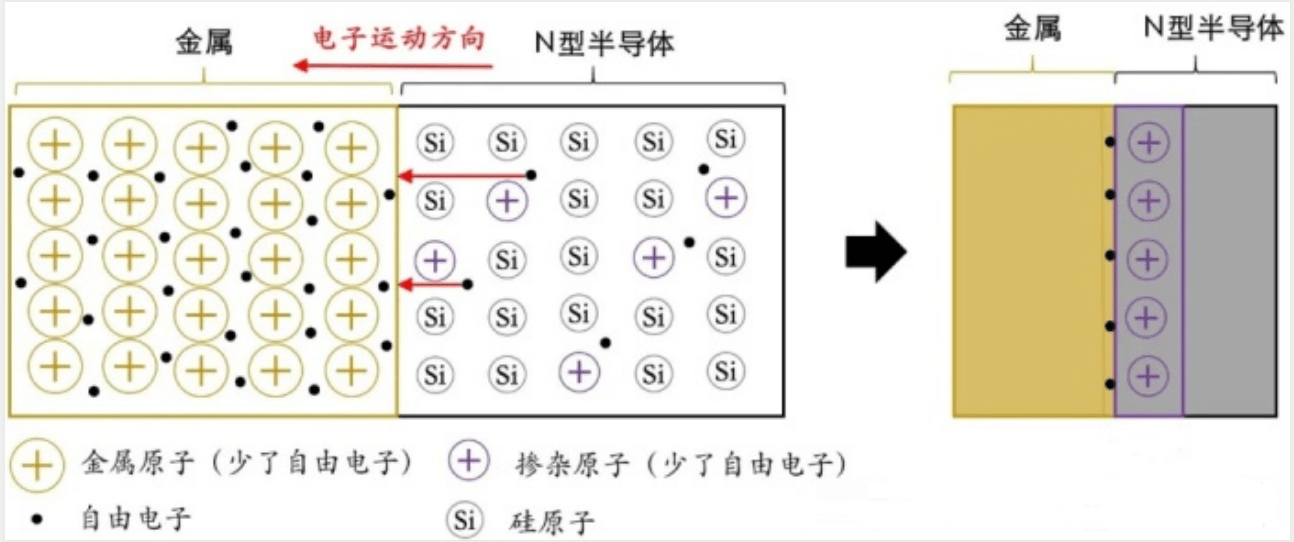
在绝对零度下,金属与半导体中的费米能级$ E_F $代表电子填充能级的水平,$E_F$以下的能级全部被电子占据,$E_F$以上的能级都是空的。在不施加高温、高压等外力条件下,金属或半导体中的大部分电子保持在低能级位置,否则,电子将获得能量,不再稳定在低能级,而是向更高能级跃迁。用$E_0$ 表示电子在真空中静止时的能量,金属中的电子从 $E_F$ 跃迁到$E_0$所需要的最小能量被称为金属的功函数,用 $W_m$ 表示,即
$$ W_m=E_0-(E_F)_m $$
类似地,当半导体中的电子获得足够的能量时也可以从半导体中逸出,半导体的功函数用$W_s$表示,计算公式为
$$ W_s=E_0-(E_F)_s $$
式中${(E_F)}s$代表半导体中的费米能级。
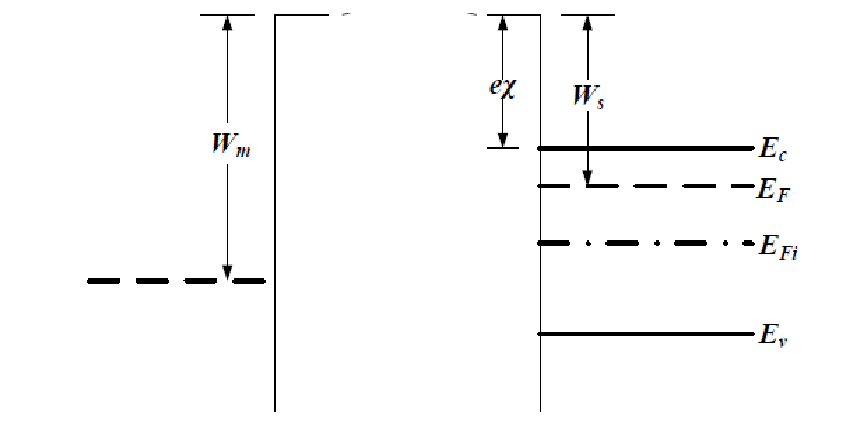
下图给出了 n 型半导体功函数与各个能级之间的关系。χ 代表电子亲合能,被定义为电子从导带底$E_C$跃迁到 $E_0$ 所需要的最小能量,计算公式如下
$$ \chi=E_0-E_c $$
n 型半导体的功函数与电子亲和能 χ 之间的关系可表示为
$$ W_s=\chi+[E_c-(E_F)_s]=\chi+E_n $$
假设半导体为 n 型半导体,当金属与半导体接触时,如果$W_m>W_s$,则半导体一侧的电子会逐渐向金属一侧流动,失去电子的半导体表面呈现正电性,获得电子的金属表面呈现负电性,随着电子的不断扩散,整个系统最终达到平衡状态,即在不施加外力的条件下金属与半导体具有统一的费米能级。平衡时由于金属与半导体两侧的正负电荷而产生内部电场,电场的正方向由半导体指向金属,此电场称为内建电场,形成的电势差叫作半导体与金属的接触电势差,用$q{V_{bi}}$来表示。在半导体一侧,由于半导体表面的电子数量比半导体内部少使得表面呈现正电性,半导体表面电子能量高于体内,能带向上弯曲,形成了势垒面,阻碍了半导体内部的电子流向半导体表面,我们称其为表面势垒层,也叫阻挡层,金属和半导体形成的这种接触就是肖特基接触。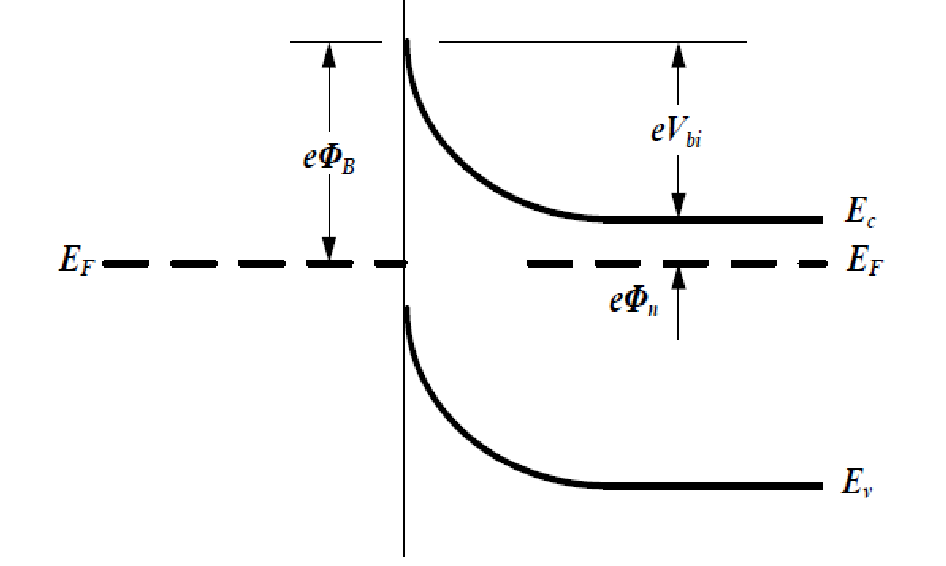
同样的对于n型半导体来说,当$W_m<W_s$时,电子从金属流向半导体,此时半导体内电场方向由表面指向体内,能带向下弯曲,表面的电子浓度远高于体内,形成了反阻挡层,反阻挡层对金属与半导体的接触电阻影响很小,此时形成的是金属半导体的欧姆接触。
金属与半导体间的肖特基势垒是指金属一侧的势垒高度,对于n型半导体,根据 Schottky–Mott 理论,肖特基势垒由下式给出:
$$ q\Phi_B=q\Phi_m-\chi_s $$
$\Phi_m$是金属的功函数,$\chi_s$是半导体的电子亲和能。
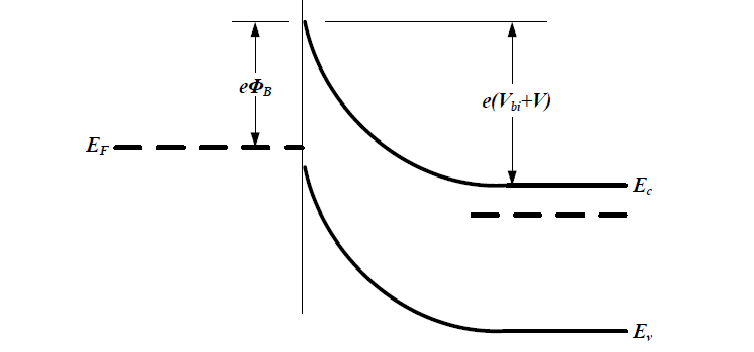
当金属接正极,半导体接负极此时结处于正偏状态。外加电压$V$后,能带不再处于平衡状态,半导体和金属之间的费米能级差等于外加的电势差,半导体一边的势垒降低$-qV$,而肖特基势垒不随电压变化,此时从半导体流向金属的电流变大,而金属流向半导体的电子不变,形成了从半导体流向金属的正向电流。电压越大,半导体势垒下降的越多,正向电流也越大,正偏时的能带图如图所示。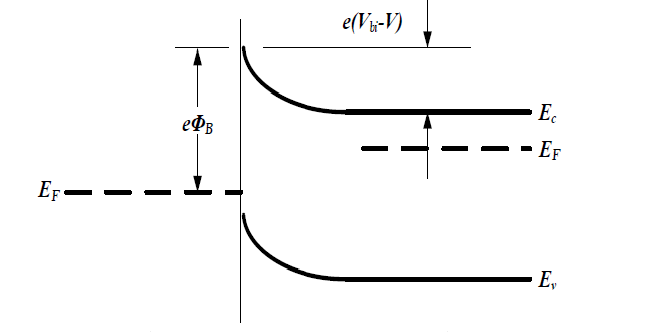
当结上加反向偏压,半导体处的势垒升高,从半导体到金属的电子减少,金属到半导体的电子占优势,但是反向偏压下,金属电子需要翻越很高的肖特基势垒$q\Phi_B$才能到达半导体,所以这一部分电子是很少的。随着电压的增大,半导体流向金属的电子可以忽略不计,此时反向电流趋向饱和值。反偏时的能带图如图所示。